9614. Размен монет

Вы работаете кассиром на веселой ярмарке, и располагаете монетами разных номиналов. Монеты каждого номинала доступны в неограниченном количестве, и стоимость каждого номинала известна. Определите количество способов, которыми можно оплатить заданную сумму, используя монеты доступных номиналов.

Например, если у Вас есть 4 номинала монет стоимостью 8, 3, 1, 2, то сумму 3 можно выдать следующими способами: {1, 1, 1}, {1, 2} и {3}.

Вход. Первая строка содержит два целых числа: сумму n (1 ≤ n ≤ 250) и количество номиналов монет m (1 ≤ m ≤ 50). Вторая строка содержит m целых чисел c_i (1 ≤ c_i ≤ 50), описывающих стоимости номиналов монет. Все значения c_i различны.

Выход. Выведите количество способов, которыми можно оплатить сумму n.

Пример входа 1	Пример выхода 1
4 3 1 2 3	4
Пример входа 2	Пример выхода 2
10 4 2 5 3 6	5

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Обозначим через f(k, n) количество способов составить сумму n из первых k номиналов монет. Это количество равно сумме двух величин:

· количества способов составить сумму n с использованием первых (k – 1) номиналов (то есть без использования k-го номинала) и

· количества способов составить сумму (n – a_k) с использованием всех k номиналов.

Таким образом, имеем соотношение:

f(k, n) = f(k – 1, n) + f(k, n – a_k)

Изначально положим f(0, 0) = 1, f(0, n) = 0 при n > 0.

Пример

Рассмотрим второй пример. В этом примере сумма n = 10, а количество номиналов k = 4. Последний номинал имеет стоимость a_k = 6. Согласно соотношению, имеем:

f(4, 10) = f(3, 10) + f(4, 4)

Сумму 10 можно составить, используя первые три номинала {2, 5, 3}, четырьмя способами:

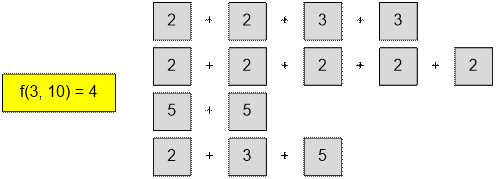
Сумму 4 можно составить с использованием всех четырех номиналов {2, 5, 3, 6} одним способом:

Реализация алгоритма

Объявим рабочие массивы.

long long dp[51][251];

int a[51];

Значение f(k, n) будем сохранять в dp[k][n].

long long f(int k, int n)

{

if (k == 0 && n == 0) return 1;

if (k == 0 || n < 0) return 0;

if (dp[k][n] != -1) return dp[k][n];

return dp[k][n] = f(k - 1, n) + f(k, n - a[k]);

}

Основная часть программы. Читаем входные данные.

memset(dp, -1, sizeof(dp));

scanf("%d %d", &n, &m);

for (i = 1; i <= m; i++)

scanf("%d", &a[i]);

Выводим искомое количество способов.

printf("%lld\n", f(m, n));

Python реализация

Значение f(k, n) будем сохранять в dp[k][n].

def f(k, n):

if k == 0 and n == 0:

return 1

if k == 0 or n < 0:

return 0

if dp[k][n] != -1:

return dp[k][n]

dp[k][n] = f(k - 1, n) + f(k, n - a[k])

return dp[k][n]

Основная часть программы. Читаем входные данные.

n, m = map(int, input().split())

a = [0] + list(map(int, input().split()))

dp = [[-1 for _ in range(n + 1)] for _ in range(m + 1)]

Выводим искомое количество способов.

print(f(m, n))